| 1.1: Review of Real Numbers and Absolute Value | 您所在的位置:网站首页 › absolute value › 1.1: Review of Real Numbers and Absolute Value |
1.1: Review of Real Numbers and Absolute Value
|
Learning Objectives Review the set of real numbers. Review the real number line and notation. Define the geometric and algebraic definition of absolute value. Real NumbersAlgebra is often described as the generalization of arithmetic. The systematic use of variables1, letters used to represent numbers, allows us to communicate and solve a wide variety of real-world problems. For this reason, we begin by reviewing real numbers and their operations. A set2 is a collection of objects, typically grouped within braces \(\{ \}\), where each object is called an element3. When studying mathematics, we focus on special sets of numbers. \[ \begin{align*} \mathbb { N } &= \underbrace{\{ 1,2,3,4,5 , \dots \}}_{\color{Cerulean}{Natural\: Numbers}} \\[4pt] W &= \underbrace{ \{ 0 , 1,2,3,4,5 , \dots \}}_{\color{Cerulean}{Whole\: Numbers}} \\[4pt] \mathbb{Z} &= \underbrace{ \{\dots ,-3,-2,-1,0,1,2,3,\dots\}}_{\color{Cerulean}{Integers}} \end{align*}\] The three periods (…) are called an ellipsis and indicate that the numbers continue without bound. A subset4, denoted \(\subseteq\), is a set consisting of elements that belong to a given set. Notice that the sets of natural5 and whole numbers6 are both subsets of the set of integers and we can write: \(\mathbb { N } \subseteq \mathbb{Z}\) and \(W \subseteq \mathbb{Z}\) A set with no elements is called the empty set7 and has its own special notation: \(\{\:\:\:\}=\varnothing\: \color{Cerulean}{Empty\: Set}\) Rational numbers8, denoted \(\mathbb{Q}\), are defined as any number of the form \(\frac { a } { b }\) where a and b are integers and b is nonzero. We can describe this set using set notation9: \(\mathbb { Q } = \left\{ \frac { a } { b } | a , b \in \mathbb { Z } , b \neq 0 \right\} \color{Cerulean}{Rational\: Numbers}\) The vertical line | inside the braces reads, “such that” and the symbol \(\in\) indicates set membership and reads, “is an element of.” The notation above in its entirety reads, “the set of all numbers \(\frac{a}{b}\) such that a and b are elements of the set of integers and b is not equal to zero.” Decimals that terminate or repeat are rational. For example, \(0.05=\frac{5}{100}\) and \(0.\overline{6}=0.6666…=\frac{2}{3} \) The set of integers is a subset of the set of rational numbers, \(\mathbb{Z}\subseteq\mathbb{Q}\), because every integer can be expressed as a ratio of the integer and 1. In other words, any integer can be written over 1 and can be considered a rational number. For example, \(7=\frac{7}{1}\) Irrational numbers10 are defined as any numbers that cannot be written as a ratio of two integers. Nonterminating decimals that do not repeat are irrational. For example, \(π=3.14159…\) and \(\sqrt{2}=1.41421…\) Finally, the set of real numbers11, denoted \(\mathbb{R}\), is defined as the set of all rational numbers combined with the set of all irrational numbers. Therefore, all the numbers defined so far are subsets of the set of real numbers. In summary,  Figure \(\PageIndex{1}\): Real Numbers Figure \(\PageIndex{1}\): Real Numbers
The set of even integers12 is the set of all integers that are evenly divisible by \(2\). We can obtain the set of even integers by multiplying each integer by \(2\). \(\{\dots, −6,−4,−2, 0, 2, 4, 6,\dots\} \color{Cerulean}{Even\: Integers}\) The set of odd integers13 is the set of all nonzero integers that are not evenly divisible by \(2\). \(\{\dots,−5,−3,−1, 1, 3, 5,\dots\} \color{Cerulean}{Odd\: Integers}\) A prime number14 is an integer greater than \(1\) that is divisible only by \(1\) and itself. The smallest prime number is \(2\) and the rest are necessarily odd. \(\{2, 3, 5, 7, 11, 13, 17, 19, 23,\dots\} \color{Cerulean}{Prime\: Numbers}\) Any integer greater than \(1\) that is not prime is called a composite number15 and can be uniquely written as a product of primes. When a composite number, such as \(42\), is written as a product, \(42=2⋅21\), we say that \(2⋅21\) is a factorization16 of \(42\) and that \(2\) and \(21\) are factors17. Note that factors divide the number evenly. We can continue to write composite factors as products until only a product of primes remains.  Figure \(\PageIndex{2}\): Prime Factorization of the number \(42\) Figure \(\PageIndex{2}\): Prime Factorization of the number \(42\)
Therefore, the prime factorization18 of \(42\) is \(2⋅3⋅7\). Example \(\PageIndex{1}\): Determine the prime factorization of \(210\). Solution Begin by writing \(210\) as a product with \(10\) as a factor. Then continue factoring until only a product of primes remains. \(210=10⋅21\) \(=2⋅5⋅3⋅7\) \(=2⋅3⋅5⋅7\) Since the prime factorization is unique, it does not matter how we choose to initially factor the number; the end result will be the same. Answer: \(2⋅3⋅5⋅7\) A fraction19 is a rational number written as a quotient, or ratio, of two integers a and b where \(b≠0\).  Figure \(\PageIndex{3}\) Figure \(\PageIndex{3}\)
The integer above the fraction bar is called the numerator20 and the integer below is called the denominator21. Two equal ratios expressed using different numerators and denominators are called equivalent fractions22. For example, \(\frac{50}{100}=\frac{1}{2}\) Consider the following factorizations of \(50\) and \(100\): \(50=2⋅25\) \(100=4⋅25\) The numbers \(50\) and \(100\) share the factor \(25\). A shared factor is called a common factor23. Making use of the fact that \(\frac{25}{25}=1\), we have \(\frac{50}{100}=\frac{2⋅ \bcancel{25}}{4⋅\bcancel{25}}=\frac{2}{4}⋅\color{Cerulean}{1}\)\(=\frac{2}{4}\) Dividing \(\frac{25}{25}\) and replacing this factor with a \(1\) is called cancelling24. Together, these basic steps for finding equivalent fractions define the process of reducing25. Since factors divide their product evenly, we achieve the same result by dividing both the numerator and denominator by \(25\) as follows: \(\frac{ 50\color{Cerulean}{÷25}}{100\color{Cerulean}{÷25}}=\frac{2}{4}\) Finding equivalent fractions where the numerator and denominator are relatively prime26, or have no common factor other than \(1\), is called reducing to lowest terms27. This can be done by dividing the numerator and denominator by the greatest common factor (GCF).28 The GCF is the largest number that divides a set of numbers evenly. One way to find the GCF of \(50\) and \(100\) is to list all the factors of each and identify the largest number that appears in both lists. Remember, each number is also a factor of itself. \(\{1,2,5,10,25,50\} \color{Cerulean}{Factors\: of \: 50}\) \(\{1,2,4,5,10,20,25,50,100\} \color{Cerulean}{Factors\: of \: 100}\) Common factors are listed in bold, and we see that the greatest common factor is \(50\). We use the following notation to indicate the GCF of two numbers: GCF\((50, 100) = 50\). After determining the GCF, reduce by dividing both the numerator and the denominator as follows: \(\frac{50\color{Cerulean}{÷50}}{100\color{Cerulean}{÷50}}=\frac{1}{2}\) Example \(\PageIndex{2}\): Reduce to lowest terms: \(\frac{108}{72}\). Solution A quick way to find the GCF of the numerator and denominator requires us to first write each as a product of primes. The GCF will be the product of all the common prime factors. \(\left. \begin{array} { l } { 108 = \color{Cerulean}{2} \cdot \color{Cerulean}{2} \cdot \color{Cerulean}{3} \cdot \color{Cerulean}{3} \cdot 3 } \\ { 72 = \color{Cerulean}{2} \cdot \color{Cerulean}{2} \cdot 2 \cdot \color{Cerulean}{3} \cdot \color{Cerulean}{3} } \end{array} \right\} \operatorname { GCF } ( 108,72 ) = \color{Cerulean}{2} \cdot \color{Cerulean}{2} \cdot \color{Cerulean}{3} \cdot \color{Cerulean}{3} = 36\) In this case, the product of the common prime factors is \(36\). \(\frac{108}{72}=\frac{108\color{Cerulean}{÷36}}{72\color{Cerulean}{÷36}}=\frac{3}{2}\) We can convert the improper fraction \(\frac{3}{2}\) to a mixed number \(1\frac{1}{2}\); however, it is important to note that converting to a mixed number is not part of the reducing process. We consider improper fractions, such as \(\frac{3}{2}\), to be reduced to lowest terms. In algebra it is often preferable to work with improper fractions, although in some applications, mixed numbers are more appropriate. Answer: \(\frac{3}{2}\) Recall the relationship between multiplication and division: In this case, the dividend29 \(12\) is evenly divided by the divisor30 \(6\) to obtain the quotient31 \(2\). It is true in general that if we multiply the divisor by the quotient we obtain the dividend. Now consider the case where the dividend is zero and the divisor is nonzero: \(\frac{0}{6}=0\) since \(6⋅0=0\) This demonstrates that zero divided by any nonzero real number must be zero. Now consider a nonzero number divided by zero: \(\frac{12}{0}= \color{Cerulean}{?}\) or \(0⋅ \color{Cerulean}{?}\) \(=12\) Zero times anything is zero and we conclude that there is no real number such that \(0⋅?=12\). Thus, the quotient \(12÷0\) is undefined32. Try it on a calculator, what does it say? For our purposes, we will simply write “undefined.” To summarize, given any real number \(a≠0\), then \(0 ÷a=\frac{0}{a}=0 \color{Cerulean}{zero}\) and \(a÷ 0=\frac{a}{0}\color{Cerulean}{undefined}\) We are left to consider the case where the dividend and divisor are both zero. \(\frac{0}{0}=\color{Cerulean}{?}\) or \(0⋅ \color{Cerulean}{?}\)\(=0\) Here, any real number seems to work. For example, \(0⋅5=0\) and also, \(0⋅ 3=0\). Therefore, the quotient is uncertain or indeterminate33. \(0÷0=\frac{0}{0} \color{Cerulean}{indeterminate}\) In this course, we state that \(0÷0\) is undefined. The Number Line and NotationA real number line34, or simply number line, allows us to visually display real numbers by associating them with unique points on a line. The real number associated with a point is called a coordinate35. A point on the real number line that is associated with a coordinate is called its graph36. To construct a number line, draw a horizontal line with arrows on both ends to indicate that it continues without bound. Next, choose any point to represent the number zero; this point is called the origin37. 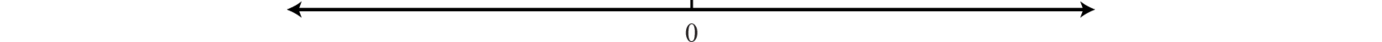 Figure \(\PageIndex{4}\) Figure \(\PageIndex{4}\)
Positive real numbers lie to the right of the origin and negative real numbers lie to the left. The number zero \((0)\) is neither positive nor negative. Typically, each tick represents one unit. 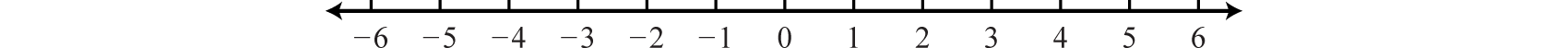 Figure \(\PageIndex{5}\) Figure \(\PageIndex{5}\)
As illustrated below, the scale need not always be one unit. In the first number line, each tick mark represents two units. In the second, each tick mark represents \(\frac{1}{7}\): 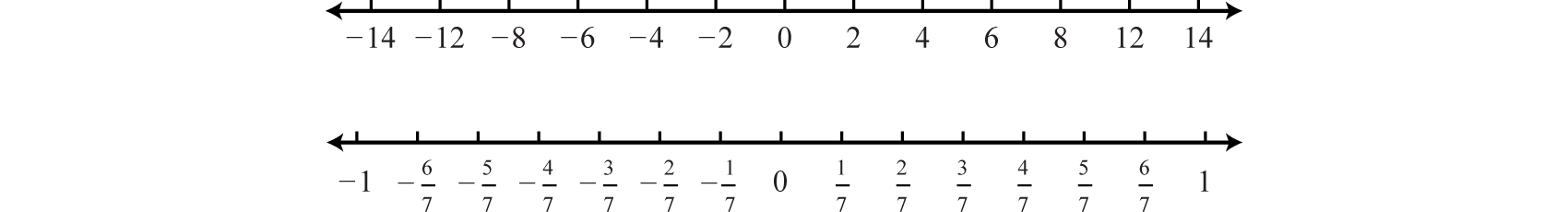 Figure \(\PageIndex{6}\) Figure \(\PageIndex{6}\)
The graph of each real number is shown as a dot at the appropriate point on the number line. A partial graph of the set of integers \(\mathbb{Z}\), follows:  Figure \(\PageIndex{7}\) Figure \(\PageIndex{7}\)
Example \(\PageIndex{3}\): Graph the following set of real numbers: \(\{−\frac{5}{2}, 0, \frac{3}{2}, 2\}\). Solution Graph the numbers on a number line with a scale where each tick mark represents \(\frac{1}{2}\) unit. Answer: 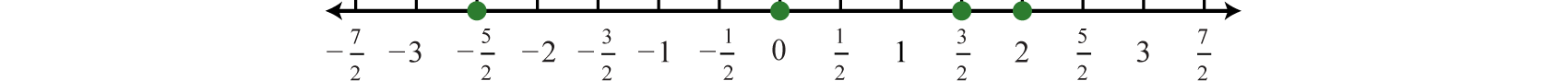 Figure \(\PageIndex{8}\) Figure \(\PageIndex{8}\)
The opposite38 of any real number a is −a. Opposite real numbers are the same distance from the origin on a number line, but their graphs lie on opposite sides of the origin and the numbers have opposite signs. 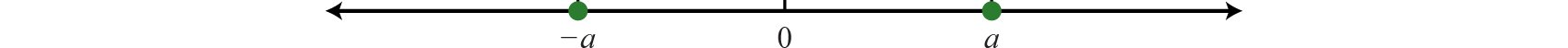 Figure \(\PageIndex{9}\) Figure \(\PageIndex{9}\)
Given the integer \(−7\), the integer the same distance from the origin and with the opposite sign is \(+7\), or just \(7\).  Figure \(\PageIndex{10}\) Figure \(\PageIndex{10}\)
Therefore, we say that the opposite of \(−7\) is \(−(−7) = 7\). This idea leads to what is often referred to as the double-negative property39. For any real number a, \(−(−a)=a\) Example \(\PageIndex{4}\): Calculate: \(−(−(−\frac{3}{8})).\) Solution Here we apply the double-negative within the innermost parentheses first. \(−(\color{Cerulean}{−(−\frac{3}{8})})=−(\frac{3}{8})\) \(=−\frac{3}{8}\) Answer: \(−\frac{3}{8}\) In general, an odd number of sequential negative signs results in a negative value and an even number of sequential negative signs results in a positive value. When comparing real numbers on a number line, the larger number will always lie to the right of the smaller one. It is clear that \(15\) is greater than \(5\), but it may not be so clear to see that \(−1\) is greater than \(−5\) until we graph each number on a number line. 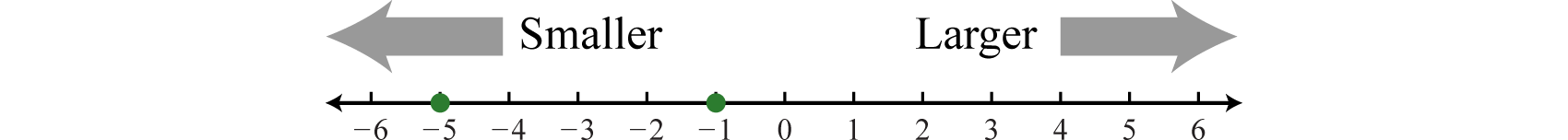 Figure \(\PageIndex{11}\) Figure \(\PageIndex{11}\)
We use symbols to help us efficiently communicate relationships between numbers on the number line. \(\color{Cerulean}{Equality Relationships Order Relationships}\) \(=\) "is equal to" \(\) "is greater than" \(\approx\) "is approximately equal to" \(\leq\) "is less than or equal to" \(\geq\) "is greater than or equal to" The relationship between the integers40 in the previous illustration can be expressed two ways as follows: \(−5−5 \color{Cerulean}{"Negative\: one\: is\: greater\: than\: negative\: five."}\) The symbols \(\) are used to denote strict inequalities41, and the symbols \(\leq\) and \(\geq\) are used to denote inclusive inequalities42. In some situations, more than one symbol can be correctly applied. For example, the following two statements are both true: \(−10\) because the graph of \(−2\) is to the right of the graph of \(−12\) on a number line. Therefore, \(−2 > −12\), which reads, “negative two is greater than negative twelve.”  Figure \(\PageIndex{12}\) Figure \(\PageIndex{12}\)
Answer: \(−2 > −12\) An algebraic inequality43, such as \(x\geq 2\), is read, “x is greater than or equal to \(2\).” Here the letter x is a variable, which can represent any real number. However, the statement \(x\geq 2\) imposes a condition on the variable. Solutions44 are the values for x that satisfy the condition. This inequality has infinitely many solutions for x, some of which are \(2, 3, 4.1, 5, 20,\) and \(20.001\). Since it is impossible to list all of the solutions, a system is needed that allows a clear communication of this infinite set. Common ways of expressing solutions to an inequality are by graphing them on a number line, using interval notation, or using set notation. To express the solution graphically, draw a number line and shade in all the values that are solutions to the inequality. This is called the graph of the solution set45. Interval and set notation follow: "x is greater than or equal to \(2\)" \(x\geq 2\)  Figure \(\PageIndex{13}\) Figure \(\PageIndex{13}\)
\(\color{Cerulean}{Interval notation:}\) \([\, 2,∞)\) \(\color{Cerulean}{Set notation:}\) \(\{x\in\mathbb{R} | x\geq 2\}\) In this example, there is an inclusive inequality, which means that the lower-bound \(2\) is included in the solution set. Denote this with a closed dot on the number line and a square bracket in interval notation. The symbol \(∞\) is read as “infinity46” and indicates that the set is unbounded to the right on a number line. If using a standard keyboard, use (inf) as a shortened form to denote infinity. Now compare the notation in the previous example to that of the strict, or noninclusive, inequality that follows: "x is less than \(3\)" \(x |
【本文地址】
.png?revision=1&size=bestfit&width=540&height=83)